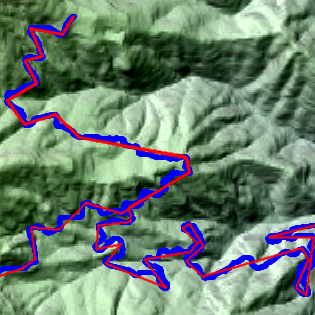
GPSトラックやルートの間引きにおいて、自作のソフトウェアで採用しているのはRamor-Douglas-Peuckerアルゴリズム。
一方、カシミール3Dや轍 wadachi、GPSBabelといった他のソフトウェアは異なるアルゴリズムを採用しており、ルートデータを間引いた際にどのような違いが生じるのか、間引き結果と処理時間を比較した。
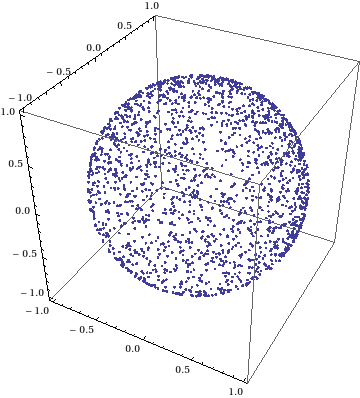
球面上に一様分布するランダムな点を生成したい時、 単純に極座標表示で$\theta$と$\varphi$を一様分布させると、極付近に点が集まってしまう。 data1 = Transpose[{Sin[t] Cos[f], Sin[t] Sin[f], Cos[t]} /. { f -> RandomReal[{0, 2 Pi}, 2000], t -> RandomReal[{0, Pi}, 2000]}]; g1 = ListPointPlot3D[data1, BoxRatios -> {1, 1, 1}] 球面上で一様分布させるには、下記のように$\theta$にArcCosを使う ($\theta$の位置の確率を$\sin\theta$に比例させたい→累積確率分布関数は$\cos$→逆関数は$\a

Nov. 29 2015: JavaScriptで実装した優先度付きキューをGitHubで公開→https://github.com/330k/priorityqueue_js/ 各ヒープのベンチマーク → http://330k.github.io/priorityqueue_js/benchmark.html これにはFibonacci Heapも比較対象に入れてある 折れ線を間引くで書いたように、 Douglas-Peuckerアルゴリズムを改良して指定した点数まで点を削減して折れ線を簡略化する場合、 優先度付きキューを使うことに

Explicit Runge-Kutta法の公式はいくつか知られているが、高次の公式になるほどButcher配列の項数が増えるため論文に誤植が多くなる。 それに気づかないまま実際に使うと、プログラムは正しく組めているはずなのに思うように精度が上がらないという落とし穴にはまってしまう。 覚書として、以下に代表的と思われる公式のButcher tableauをまとめる。 以下のButcher tableauはMathemati
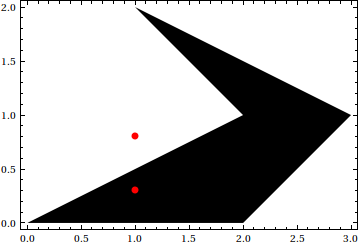
ある点が多角形の内側にあるのか外側にあるのかを判定するには主に ある点から直線をひいて多角形の辺と何回交差するか判定する(偶数回なら外、奇数回なら中) ある点から多角形の各頂点を順番に見ていったときに何回転するか の2つの方法がある。 しかし辺との交差回数をカウントするのは、直線と辺が平行だったり、頂点で交差したりする場合などに特別な配慮が必要なので、 ここでは2番目の方法で実装する。 点から多角形上の点を順
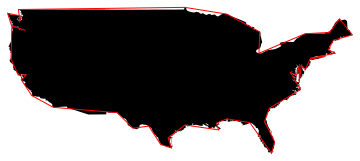
読み込んだGPSログのデータを間引きたい、と思って調べたところ、
(Ramer-)Douglas-Peuckerのアルゴリズムというものがあることが分かった。
基本的な考え方は、
- 折れ線の始点と終点を結ぶ線分と各点の距離を求める。
- すべての点との距離が許容誤差$\varepsilon$以内に入っていれば始点と終点だけを返して終了。
- そうでなければ距離が最大の点Pを選択。
- 始点から点Pまでの折れ線と、点Pから終点までの折れ線のそれぞれについてまた1から処理する。
という再帰的なもの。
再帰的なものはMathematicaの得意分野なので、MathematicaでRamer-Douglas-Peuckerのアルゴリズムを実装してみた。






