Douglas-Peucker向けの優先度付きキュー実装の検討
Nov. 29 2015:
- JavaScriptで実装した優先度付きキューをGitHubで公開→https://github.com/330k/priorityqueue_js/
- 各ヒープのベンチマーク → http://330k.github.io/priorityqueue_js/benchmark.html これにはFibonacci Heapも比較対象に入れてある
折れ線を間引くで書いたように、 Douglas-Peuckerアルゴリズムを改良して指定した点数まで点を削減して折れ線を簡略化する場合、 優先度付きキューを使うことになる。
このアルゴリズムでは
- 始点と終点を結ぶ線分で最も距離が大きな点$P_1$を選ぶ
- 始点と点$P_1$を結ぶ線分で距離最大となる点$P_2$をキューに登録(優先度は点$P_2$と線分の距離)
- 点$P_1$と終点を結ぶ線分で距離最大となる点$P_3$をキューに登録(優先度は点$P_3$と線分の距離)
- キューから距離が最大(=優先度最大)の点を選んで、2に戻る
という手順となるため、「キューに2つ登録して、1つ取り出す」ということを繰り返すことになる。
そこで今回はランダムな優先度のデータを
- 連続して登録し、連続して取り出す(要はソートしているだけ)
- 「キューに2つ登録して、1つ取り出す」を繰り返すDouglas-Peuckerを想定した試験
という操作に対してどの優先度付きキューの実装が良い性能をしめすのか、ベンチマークを取ってみた。
優先度付きキューの実装にはいくつか方法があるが、今回は以下の6種類を試してみた。
- Array.sort(): キューへの追加はArray.push()、キューから取り出すときに必要であればArray.sort()してArray.pop()する。非常に単純で楽チン。結果の検証用。
- Selection: キューへの追加はArray.push()、キューから取り出すときに最大要素を選択。enqueue: $O(1)$, dequeue: $O(n^2)$。
- Insertion: キューへの追加時に挿入ソートを行う。キューから取り出すときはArray.pop()するだけ。enqueue: $O(n^2)$, dequeue: $O(1)$。
- Binary Insertion: キューへの追加時に二分挿入ソートを行う。あとは3と同じ。enqueue: $O(n^2)$, dequeue: $O(1)$。
- Binary Heap: 二分ヒープ(wikipedia)での実装。ポインタなしで実装できるので省メモリ。java.util.PriorityQueueはこれらしい。enqueue: $O(\log n)$, dequeue: $O(\log n)$。
- Pairing Heap: ペアリングヒープ(wikipedia: en)での実装。gcc(libstdc++)のpriority_queueはこれらしい。enqueue: $O(1)$, dequeue: $O(\log n)$。実装にはこれを参考にした。
いずれもJavaScriptで実装した。
ベンチマーク結果
以下、Firefox 29とChromium 34での結果。単位はmsで、小さいほうが高速。 載せていないがVirtualBox上のWindows XPで測定してもほぼ同じ結果だった。
Firefox 29 on Ubuntu 12.04 LTS 64bit
Sequential
| n | Array.sort() | Selection | Insertion | Binary Insertion | Binary Heap | Pairing Heap |
|---|---|---|---|---|---|---|
| 1000 | 3 | 4 | 3 | 1 | 2 | 2 |
| 2000 | 2 | 14 | 8 | 1 | 1 | 1 |
| 5000 | 3 | 88 | 49 | 4 | 2 | 2 |
| 10000 | 7 | 346 | 185 | 11 | 4 | 5 |
| 20000 | - | 1307 | 744 | 32 | 8 | 10 |
| 50000 | - | - | - | 177 | 22 | 26 |
| 100000 | - | - | - | 688 | 48 | 66 |
| 200000 | - | - | - | 2909 | 128 | 164 |
| 500000 | - | - | - | - | 413 | 512 |
| 1000000 | - | - | - | - | 996 | 1235 |
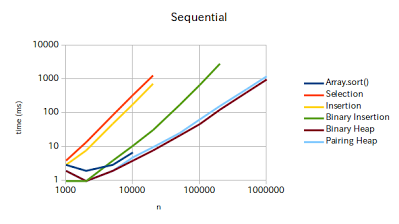
Dauglas-Peucker (2-enqueue, 1-dequeue)
| n | Array.sort() | Selection | Insertion | Binary Insertion | Binary Heap | Pairing Heap |
|---|---|---|---|---|---|---|
| 1000 | 15 | 3 | 2 | 1 | 1 | 1 |
| 2000 | 49 | 9 | 6 | 1 | 0 | 1 |
| 5000 | 274 | 47 | 36 | 1 | 3 | 1 |
| 10000 | 1107 | 180 | 128 | 4 | 4 | 2 |
| 20000 | - | 685 | 554 | 13 | 9 | 6 |
| 50000 | - | - | - | 53 | 21 | 15 |
| 100000 | - | - | - | 189 | 45 | 36 |
| 200000 | - | - | - | 719 | 102 | 78 |
| 500000 | - | - | - | - | 313 | 250 |
| 1000000 | - | - | - | - | 729 | 592 |
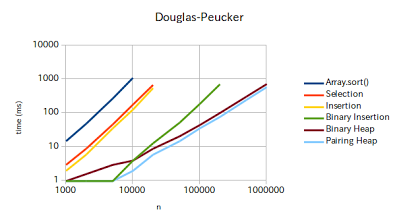
Chromium 34 on Ubuntu 12.04 LTS 64bit
Sequential
| n | Array.sort() | Selection | Insertion | Binary Insertion | Binary Heap | Pairing Heap |
|---|---|---|---|---|---|---|
| 1000 | 5 | 11 | 7 | 2 | 2 | 5 |
| 2000 | 3 | 33 | 17 | 2 | 2 | 2 |
| 5000 | 3 | 211 | 104 | 6 | 7 | 4 |
| 10000 | 6 | 921 | 428 | 13 | 10 | 10 |
| 20000 | - | 3238 | 2083 | 38 | 21 | 21 |
| 50000 | - | - | - | 210 | 63 | 66 |
| 100000 | - | - | - | 924 | 157 | 167 |
| 200000 | - | - | - | 6875 | 393 | 383 |
| 500000 | - | - | - | - | 1289 | 1207 |
| 1000000 | - | - | - | - | 2917 | 2779 |
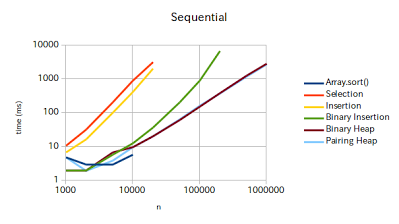
Dauglas-Peucker (2-enqueue, 1-dequeue)
| n | Array.sort() | Selection | Insertion | Binary Insertion | Binary Heap | Pairing Heap |
|---|---|---|---|---|---|---|
| 1000 | 33 | 4 | 3 | 0 | 1 | 0 |
| 2000 | 119 | 17 | 13 | 2 | 2 | 0 |
| 5000 | 913 | 102 | 76 | 3 | 5 | 3 |
| 10000 | 4008 | 435 | 309 | 6 | 10 | 7 |
| 20000 | - | 1663 | 1501 | 16 | 21 | 10 |
| 50000 | - | - | - | 138 | 61 | 37 |
| 100000 | - | - | - | 581 | 147 | 100 |
| 200000 | - | - | - | 2298 | 321 | 206 |
| 500000 | - | - | - | - | 996 | 605 |
| 1000000 | - | - | - | - | 2203 | 1492 |
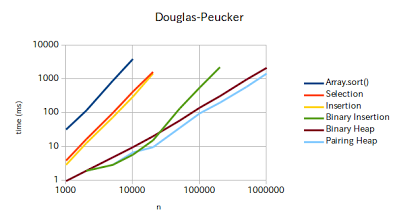
ということで、上記の表からわかるのは、
- Google Mapsで作ったルートやGPSのログ(代表的なロガーの記録点数は10万〜20万)を処理することを考えると、Array.sort()やSelection(選択ソート)、Insertion(挿入ソート)では遅すぎる。
- Binary Insertion(二分挿入ソート)なら点の数が少なければ許容できるかも。
- Binary Heapでの連続的な(Sequential)操作に対しては、FirefoxではPairing Heapよりも高速だが、ChromiumではPairing Heapよりも遅い。
- 「2つ加えて1つ取る」操作に対してはPairing HeapのほうがBinary Heapより高速。
- 全体として、Firefoxのほうが2〜3倍高速。
といったところ。
結論
以上より、Douglas-Peuckerを改良したアルゴリズムで使う優先度付きキューの実装は、Pairing Heapが良いようだ。
補足
さらに他のヒープでの実装を試してみた。
またスマートフォン(URBANO L01、Android 4.2)でもベンチマークを取ってみた。
Sequential
| n=1000000 | Pairing Heap | Binary Heap | d-ary Heap (d=3) | d-ary Heap (d=4) | Skew Heap | Leftist Heap |
|---|---|---|---|---|---|---|
| Firefox 29 on Ubuntu 12.04 | 1237 | 974 | 886 | 822 | 1791 | 1904 |
| Chromium 34 on Ubuntu 12.04 | 2740 | 2909 | 2852 | 2846 | 4867 | 5080 |
| Firefox 29 on Android 4.2 | 9270 | 9730 | 9369 | 8905 | 26907 | 37929 |
| Chrome 35 on Android 4.2 | 25851 | 29397 | 27159 | 24713 | 35926 | 48263 |
Dauglas-Peucker (2-enqueue, 1-dequeue)
| n=1000000 | Pairing Heap | Binary Heap | d-ary Heap (d=3) | d-ary Heap (d=4) | Skew Heap | Leftist Heap |
|---|---|---|---|---|---|---|
| Firefox 29 on Ubuntu 12.04 | 590 | 697 | 612 | 558 | 803 | 838 |
| Chromium 34 on Ubuntu 12.04 | 1251 | 2146 | 2103 | 1956 | 1911 | 2280 |
| Firefox 29 on Android 4.2 | 4609 | 6731 | 5697 | 5640 | 17942 | 8418 |
| Chrome 35 on Android 4.2 | 11902 | 26250 | 24070 | 22631 | 14342 | 21853 |
d-ary Heap(d=4)はUbuntuのFirefoxにおいて最も良い性能を示した。
AndroidのFirefoxやChromiumではBinary Heapよりは高速だったが「2つ加えて1つ取る」操作においてPairing Heapは超えられなかった。 Skew HeapやLeftist Heapは特に連続的な操作に対して弱いようだ。
総じてPairing Heapか、d-ary Heap(d=4)が高速といえる。