折れ線を間引く(Ramer-Douglas-Peuckerアルゴリズム)

October 24, 2009 (Last Modified: May 30, 2023)

雑記帳

読み込んだGPSログのデータを間引きたい、と思って調べたところ、 (Ramer-)Douglas-Peuckerのアルゴリズムというものがあることが分かった。

基本的な考え方は、

折れ線の始点と終点を結ぶ線分と各点の距離を求める。
すべての点との距離が許容誤差$\varepsilon$以内に入っていれば始点と終点だけを返して終了。
そうでなければ距離が最大の点Pを選択。
始点から点Pまでの折れ線と、点Pから終点までの折れ線のそれぞれについてまた1から処理する。

という再帰的なもの。

再帰的なものはMathematicaの得意分野なので、MathematicaでRamer-Douglas-Peuckerのアルゴリズムを実装してみた。

線分と点の距離

さて、まずは線分と点の距離を求める関数を作成する。

ネットで検索すると直線と点の距離を用いているものが多いが、線分と点の距離のほうが形状をよく保存できるのではないだろうか、と個人的に考えている。

線分ABに点Pから下ろした垂線の足が点Hだとすると、

線分ABと直線PHは直交 ⇔ 内積が0 ($\overrightarrow{AB} \cdot \overrightarrow{PH} = 0$)
点Hは直線AB上にある ⇔ 実数$t$に対して$t \overrightarrow{AB} = \overrightarrow{AH}$

の条件から、Hの座標と実数tの値が求まる。 Mathematicaを使うと

A = {ax, ay}; B = {bx, by}; P = {px, py}; H = {x, y};

Solve[{
     (B - A).(H - P) == 0,
     H == A + (B - A) t
     }, {x, y, t}][[1]] // FullSimplify
{x -> (ay^2 bx + ax^2 px + ax ay (-by + py) - 
     ay bx (by + py) + ax (by^2 - 2 bx px - by py) + 
     bx (bx px + by py))/((ax - bx)^2 + (ay - by)^2), 
 y -> ((ax - bx) (by (ax - px) + ay (-bx + px)) + (ay - 
      by)^2 py)/((ax - bx)^2 + (ay - by)^2), 
 t -> (ax^2 + ay^2 + bx px - ax (bx + px) + by py - 
   ay (by + py))/((ax - bx)^2 + (ay - by)^2)}

となる。これは2次元の場合だが、一般に

$t = (\boldsymbol{A}-\boldsymbol{B}) \cdot (\boldsymbol{A}-\boldsymbol{P}) / (\boldsymbol{A}-\boldsymbol{B}) \cdot (\boldsymbol{A}-\boldsymbol{B})$
$\boldsymbol{H} = \boldsymbol{A} + t(\boldsymbol{B}-\boldsymbol{A})$

となるので、3次元以上の場合はこれから計算すればよい。

実数$t$が0から1までの間にあるとき、垂線の足、点Hは線分AB上にある。

よって線分ABと点Pの距離は

$0 \leq t \leq 1$ならばHP
$t<0$ならばAP
$1<t$ならばBP

となる。以上を実装すると、

SegmentPointDistance[{ax_, ay_}, {bx_, by_}, {px_, py_}] := Module[
  {x, y, t},
  t = ((ax - bx)(ax - px) + (ay - by)(ay - py)) / ((ax - bx)^2 + (ay - by)^2);
  x = ax - (ax - bx) t;
  y = ay - (ay - by) t;
  Which[
   TrueQ[0 <= t <= 1], Norm[{x, y} - {px, py}],
   TrueQ[1 < t], Norm[{bx, by} - {px, py}],
   True, Norm[{ax, ay} - {px, py}]
   ]
  ]

となる。点Aと点Bが一致してしまう場合は0による除算が発生するので注意。

折れ線を間引く

これで本題に入れる。とはいっても最初のアルゴリズムを素直に実装すればよく、

LineSimplify[{p1 : {_, _}, midpoints : {_, _} .., p2 : {_, _}}, epsilon_] := Module[
  {distance, maxdistance, maxdistanceposition},
  distance = SegmentPointDistance[p1, p2, #] & /@ {midpoints};
  maxdistanceposition = Ordering[distance, -1][[1]];
  maxdistance = distance[[maxdistanceposition]];
  If[TrueQ[maxdistance < epsilon],
   {p1, p2},
   Join[
    LineSimplify[
     Join[{p1}, {midpoints}[[1 ;; maxdistanceposition]]], epsilon],
    Rest[LineSimplify[
      Join[{midpoints}[[
        maxdistanceposition ;; -1]], {p2}], epsilon]]
    ]
   ]
  ]
LineSimplify[{p1 : {_, _}, p2 : {_, _}}, epsilon_] := {p1, p2}

となる。距離の最大値と最大値を与える点の番号を別々に求めているところがちょっと冗長だが仕方ない。

例

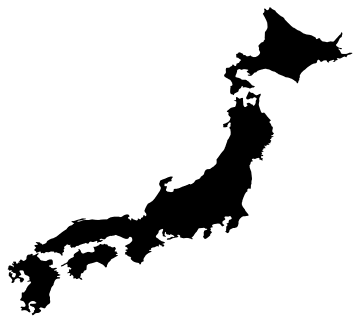
MathematicaのCountryDataから取り出せる日本の形状データを使ってこのアルゴリズムをテストしてみた例。¹

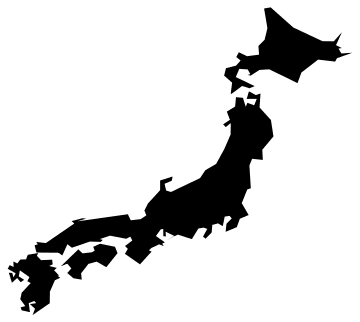
間引き前(2005点)	間引き後(212点) $\varepsilon$=0.1

間引いた後の点の数を指定できるようにするには

さて、元々のDouglas-Peuckerのアルゴリズムは許容誤差$\varepsilon$を与えて間引くので、間引いた後の点の数がいくらになるのかは指定できない。

しかし、実際の用途(地図表示時の動作を軽くしたい、GPSデバイスにインポートしたい、etc)では間引き後の点数を指定できたほうが便利である。

これを実現するには、以下のようなアルゴリズムになる。

始点Aと終点Bを結ぶ線分と各点の距離を求める
距離が最大の点Pとその距離の情報を優先度付きキューに加える
優先度付きキューからもっとも距離の大きい要素を取り出し、その点を残す点として登録する
点Aを始点、点Pを新たな終点として、最大距離を与える点とその距離を優先度付きキューに加える
点Pを新たな始点、点Bを終点として、最大距離を与える点とその距離を優先度付きキューに加える
リストが空になるか、点の個数が指定した数になるまで3以降を繰り返す。
残す点として登録したものだけを取り出す

というアルゴリズムになる。

GPXデータを簡略化ではこれを実装した。

Jun. 26 2014 追記:

Mathematica 8で実装してみた。簡単のため優先度付きキューではなく配列を毎回Sortしている。

SegmentPointDistance2 = 
  Compile[{{a, _Real, 1}, {b, _Real, 1}, {p, _Real, 1}}, 
   Module[{ax, ay, bx, by, px, py, x, y, t},
    ax = a[[1]]; ay = a[[2]];
    bx = b[[1]]; by = b[[2]];
    px = p[[1]]; py = p[[2]];
    t = ((ax - bx)(ax - px) + (ay - by)(ay - py)) / ((ax - bx)^2 + (ay - by)^2);
    x = ax - (ax - bx) t;
    y = ay - (ay - by) t;
    Which[
     0 <= t <= 1, Sqrt[((x - px)^2 + (y - py)^2)],
     1 < t, Sqrt[((bx - px)^2 + (by - py)^2)],
     True, Sqrt[((ax - px)^2 + (ay - py)^2)]
     ]
    ]
   , Parallelization -> True
   , RuntimeAttributes -> {Listable}
   ];
findFarthest[data_, pos1_, pos2_] /; pos2 - pos1 >= 2 := 
  Module[{dist, maxdist, maxpos},
   dist = 
    SegmentPointDistance2[data[[pos1]], data[[pos2]], 
     data[[pos1 + 1 ;; pos2 - 1]]];
   maxpos = Ordering[dist, -1][[1]];
   maxdist = dist[[maxpos]];
   {maxdist, pos1, pos1 + maxpos, pos2}
   ];
findFarthest[data_, pos1_, pos2_] := Sequence[];
lineSimplifyNStep[data_, {first_, rest___}] := 
 Module[{dist, pos1, maxpos, pos2},
  {dist, pos1, maxpos, pos2} = first;
  Sow[maxpos];
  Reverse@Sort[
     {rest,
     findFarthest[data, pos1, maxpos],
     findFarthest[data, maxpos, pos2]
     }]
  ];
LineSimplifyN[line : {{_, _} ..}, n_ /; n <= 0] := {};
LineSimplifyN[line : {{_, _} ..}, 1] := {First[line]};
LineSimplifyN[line : {{_, _} ..}, 2] := {First[line], Last[line]};
LineSimplifyN[line : {{_, _} ..}, n_] /; Length[line] <= n := line;
LineSimplifyN[line : {{_, _} ..}, n_Integer] := 
  line[[{1, Sequence @@ Sort[
       Reap[Nest[lineSimplifyNStep[line, #] &,
          {findFarthest[line, 1, Length[line]]}, n - 2]][[2, 1]]
       ], Length[line]}]];

アメリカ合衆国のデータを使った例が以下。

line = CountryData["USA", "Polygon"][[1, 1]];
Graphics[{Polygon[line], Red, Line@LineSimplifyN[line, 50]}]

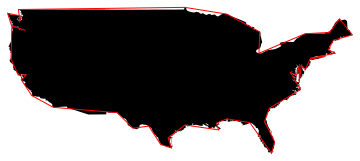
元は4672点、赤線が50点に削減したもの。

May 26 2023: 追記:

Mathematica 12.1で優先度付きキューが実装された(PriorityQueue—Wolfram言語ドキュメント)ので、それを使った実装。

LineSimplifyN2[line:{{_, _} ..}, n_Integer] := Module[{queue, result, count, v},
  queue = CreateDataStructure["PriorityQueue", {}, Order[First[#1], First[#2]]&];
  queue["Push", findFarthest[line, 1, Length[line]]];
  result = {1, Length[line]};
  While[Length[result] < n,
    v = queue["Pop"];
    AppendTo[result, v[[3]]];
    
    If[v[[3]] - v[[2]] >= 2, queue["Push", findFarthest[line, v[[2]], v[[3]]]]];
    If[v[[4]] - v[[3]] >= 2, queue["Push", findFarthest[line, v[[3]], v[[4]]]]];
  ];
  line[[ Sort[result] ]]
]

地理データを間引く場合は「線分と点の距離を求める際に垂線を下ろす」ということをしている以上、本来は少なくともメルカトル図法などの正角図法で投影した座標値を使って間引くのが適切だと考えられる。
ここでは緯度経度の値をそのまま使った(正距円筒図法 - Wikipedia)。 ↩︎