Mathematica

Mathematicaのシンボルにはいくつかの属性を設定でき、ReadProtected属性を付与することで定義を隠蔽することができるが、 DownValuesやUpValuesを使うことで定義を表示することができる他、TraceやTracePrintを使うことで内部処理を追跡することが可能である。

そこで、ReadProtected属性に加えてLocked属性を付与することで内部処理を隠蔽することができる。

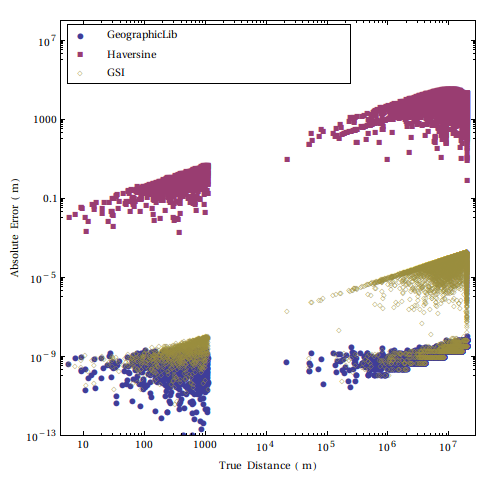
2地点の緯度経度を与えてその間の距離を求める計算式はいくつかあり、 GeoDistanceとその他の測地線距離算出式の精度 ではランダムな2点間の距離や、日本での運転経路データを用いて代表的な計算式の精度を評価したが、 短い距離の計算精度の評価と、対蹠点付近の計算精度の評価が不十分であった。

そこで、比較する計算式を追加した上で、GeographicLibのテストデータを用いて計算精度の再評価を行った。

Mathematicaのプログラムを難読化し、またそこに隠しメッセージを埋め込む手法をいくつか検討してみた。

円周率をモンテカルロ法で求めるプログラムを難読化し、隠しメッセージを埋め込む例をいくつか考えた。

Ubuntuのアップデート時にMathematicaノートブックをNautilusから起動できなくなってしまって少し面倒だったので、再度設定を行った。

ついでに、すでにMathematicaが起動している時に2つ目のノートブックをNautilusから開いた時、デフォルトでは別プロセスのMathematicaが起動してしまってライセンスが要求されてしまう点にも対処した。

Mathematicaの省略記法はドキュメントやヘルプで調べにくいのでまとめてみる。 関数適用 @ (前置記法) f@aはf[a]と等価。 後ろのカッコ(])を入力しなくてもすむ。 Plot[Evaluate@Integrate[x^2, x], {x, -3, 3}] // (後置記法) a // fはf[a]と等価。 数値にする(N)や簡約化(Simplify、FullSimplify)でよく使う。 In[1]:= Sin[2] // N Out[1]= 0.909297 ~ ~ (中置記法) a~f~bとすると、f[a, b]と等価になる。 In[1]:= {1, 2}~Join~{3, 4} Out[1]= {1, 2, 3, 4} 関数適用

MathematicaからCUDAを使いたかったので、GPU搭載のノートPCを購入してセットアップした。 購入PC PC工房のGeForce 1060搭載ノートPC(OSなし) : STYLE-15FX093-i7-RNFR [OS LESS] CPU: Intel Core i7-7700HQ 2.8GHz Memory: 16GB Storage: SSD 240GB + HDD 2TB GPU: NVIDIA GeForce 1060 6GB Ubuntu 17.10 日本語Remixをダウンロード 旧PC(Ubuntu 16.04)で Ubuntu Desktop 日本語 Remixのダウンロードから、ubuntu-ja-17.10-desktop-amd64.isoをダウンロー

Unicode制御文字のうち、LRO(Left-to-right override, U+202D)とRLO(Right-to-left override, U+202E)は行中でも文字列の方向を変更する。 1行の中に何度もLROとRLOが入ると、カーソルキーが踊って楽しいことになる。 例えば、下のテキストの中でカーソルを動かしたり、文字列を選択しようとしても上手くできないはず。 ‮‭い‮を‭ろ‮る‭は‮ぬ‭に‮り‭ほ‮ち‭へ‮と ‮‭わ‮む‭

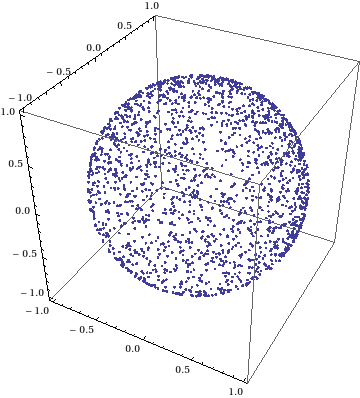
球面上に一様分布するランダムな点を生成したい時、 単純に極座標表示で$\theta$と$\varphi$を一様分布させると、極付近に点が集まってしまう。 data1 = Transpose[{Sin[t] Cos[f], Sin[t] Sin[f], Cos[t]} /. { f -> RandomReal[{0, 2 Pi}, 2000], t -> RandomReal[{0, Pi}, 2000]}]; g1 = ListPointPlot3D[data1, BoxRatios -> {1, 1, 1}] 球面上で一様分布させるには、下記のように$\theta$にArcCosを使う ($\theta$の位置の確率を$\sin\theta$に比例させたい→累積確率分布関数は$\cos$→逆関数は$\a

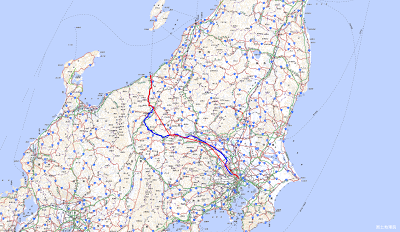
GPSロガー(Holux m-241)のメモリが破損しているのか、 実は6月30日と7月3日の軽井沢→直江津ツーリングと、9月の西九州→佐多岬ツーリングでは、 ログが破損していたため、Googleのロケーション履歴を代用している。 バイナリデータは一応吸い出せているようなので、その構造を調べると、 HOLUX m-241 LoggerUtility .trlファイル構造の覚書 より以下のような構造になっている。 1レコード20バイトの固定長 時刻4バイト 緯度

Mathematica 8から、CompileでCコンパイラを使って直接ネイティブコードにコンパイルできるようになった。 使用するCコンパイラは、 Needs["CCompilerDriver`"]; CCompilerDriver`$CCompiler = { "Name" -> "GCC", "Compiler" -> CCompilerDriver`GCCCompiler`GCCCompiler, "CompilerInstallation" -> "/usr/bin", "CompilerName" -> Automatic }; というように、CCompilerDriver`$CCompilerを変更して指定する。 以前からのCompile(“WVM”)と、各コンパイラの比較のため、ベンチマークを行ってみた。 検証環境は以下の通り。 CPU: Intel Core-i7 3770 (インテル