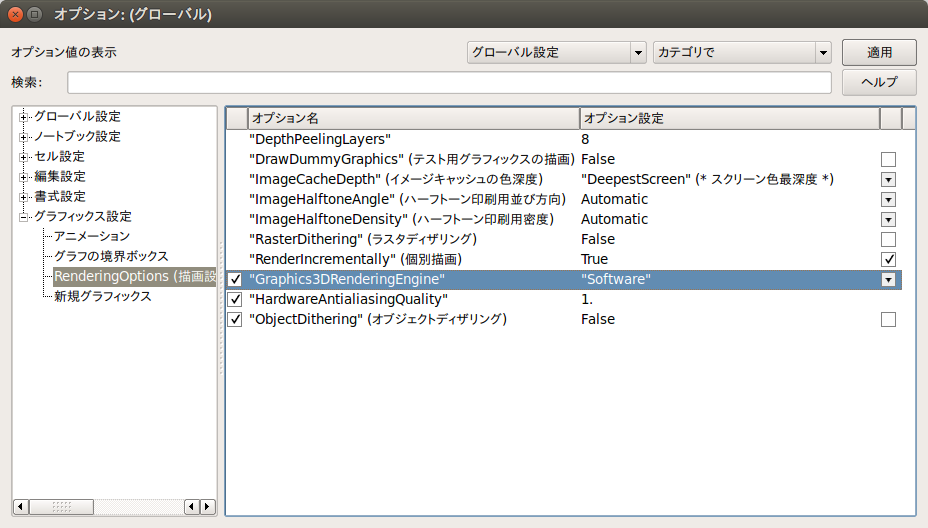
たまたま私の環境の問題かもしれないが、 Intel Core-i7 3770 Ubuntu 14.04 LTS Mathematica 8.0.4 Home Edition という環境で、Mathematicaのノートブック上でPlot3DなどのGraphics3Dオブジェクトが、 うまく表示できないことに悩まされていたが、その解決法が分かった。 メニューの「編集」→「環境設定」から、「詳細」タブを開き、「オプションインスペクタを開く」をクリック。 オプションインスペクタでは「グラフィックス設定」「Rendering
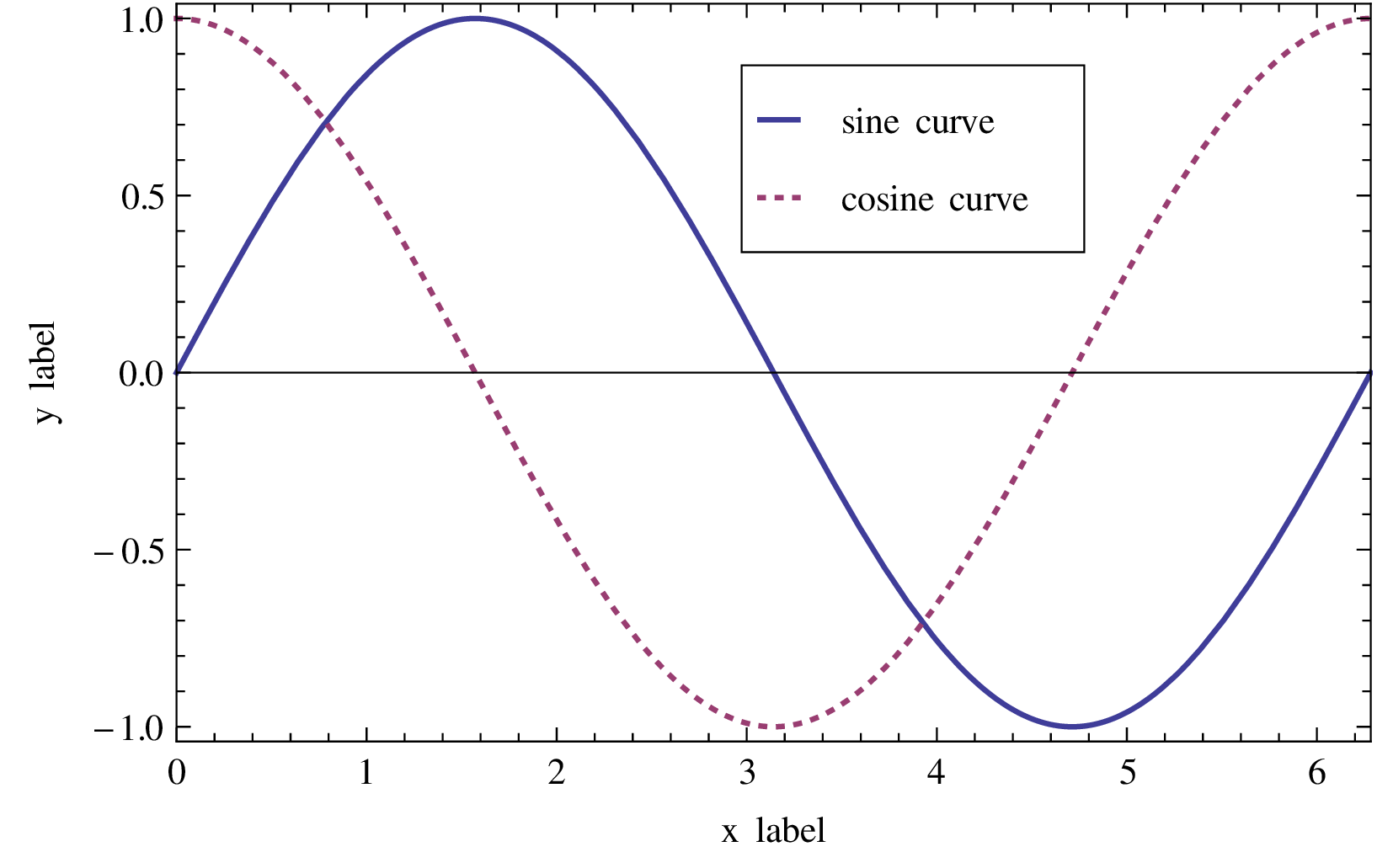
Mathematicaで作る図やグラフは美しいんだ！ということを伝えたいので、 もう数年も前になるが、修士論文を書くときにMathematicaで作るグラフにこだわった点を思い出しながらまとめてみる。 論文を書くために使うソフトウェア 私はpLaTeXで論文を書いたが、研究室ではWordが推奨されていた。 図表の番号を管理する必要や図表の位置がずれて飛んでいってしまうといった事態も起きないし、目次や索引、
拙作のリバーシプログラムViglaは高校時代に作ったものだが、 評価関数は手の広さと辺の形を適当に数値化したものであるためにあまり強いプログラムにはできなかった。 当時から強いリバーシプログラムは辺や隅のパターンを評価していることは知ってはいたものの、理解出来ずじまいだった。 今回もう一度挑戦してみようと思い、まずはMathematicaでパーセプトロンとバックプロパゲーションによる学習を実装してみた。
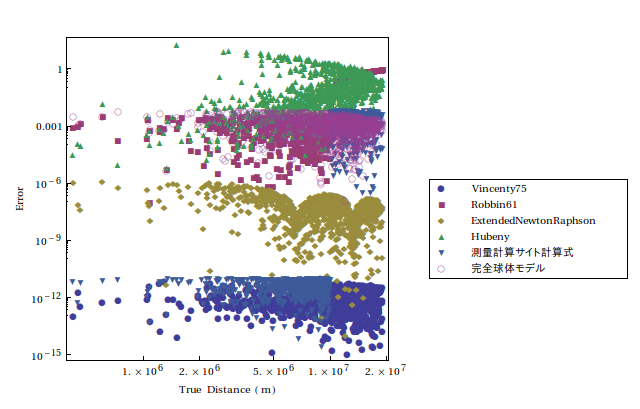
Mathematicaには2点の緯度と経度を与えて、その間の測地線距離を返す関数としてGeoDistanceがある。
しかしながら、ここで書かれているように、その精度には疑問が呈されているようだ。
17 Mar. 2022 追記)
続編記事を投稿
Wolfram CDF Player を汎用するにあるように、 CDF PlayerでもJ/Linkを使えばローカルファイルの読み込み、書き込みができる(※CDFファイルの作成にはMathematicaが必要)。 上記リンク先ではテキストファイルを読み込む例が載っているが、バイナリファイルとして読み込んでImportStringを使えば、 Mathematicaが対応している形式すべてのファイルを読み込むことができる。 J/Linkでバイナリ
MathematicaのExportでAVIなどの動画ファイルを作成することは簡単に可能だが、 いかんせんすべてのフレームの画像を作成してからファイルに書きだすので、フレーム数に比例してメモリの使用量が多くなってしまう。 そのため長いムービーの作成は困難であった。 そこで、ffmpegと併用することでメモリ使用量を抑えつつ、長編の動画ファイルを制作する。 具体的には、 ffmpegで標準入力から読み込ませる
ドキュメントにはないものの、MathematicaではSQLiteを扱うことができる。 しかしながら、BLOB型や文字列で日本語などを扱うには少し工夫が必要なので、メモ。 BLOB型 select 直接BLOB型をselectすると$Failedが返ってくるので、hex関数で16進文字列として返す。 db = Database`OpenDatabase[sqlitefilepath]; rs = Database`QueryDatabase[db, "select hex(column_name) from table_name"]; これを16進文字列→数値→バイト列→文字列と変換して、最後にImportStringで読み込むと、
Mathematica 8 Home Edition 日本語版をUbuntu 12.04 LTS 64bit版にインストールしたところ、 ディレクトリ、ファイル名に日本語が含まれるノートブックファイル(.nb)を開けない ディレクトリ、ファイル名に日本語が含まれるとImport/Exportできない、FileNamesで列挙できない ノートブック中に日本語を入力できない $SystemCharacterEncoding、$CharacterEncodingが"
Mathematicaにおいてプログラムの実行速度を最適化する際の項目を思いつく限り挙げてみた。 関数型パラダイムで書く 必然的に組み込み関数を多く使い、リストをまとめて操作することになるので手続き型で書くより速くなることが多い。 コード量も少なくなって読みやすくなるので、よほどのことでない限りMathematicaでは関数型で書く。 具体的には、手続き型ループ構文(Do, For, Whileなど)をやめて、Ma
MathematicaではImportやExportを使って様々な形式のファイルを読み書きできるが、 標準で対応していないファイル形式についても自分でローダやライタを作り、 それをImportやExportに対応させる方法がExtending Import & Export (Wolfram Library Archive)において解説されている。 しかしこの文書は2003年のもので以前はExperimental`RegisterConverterという関数で