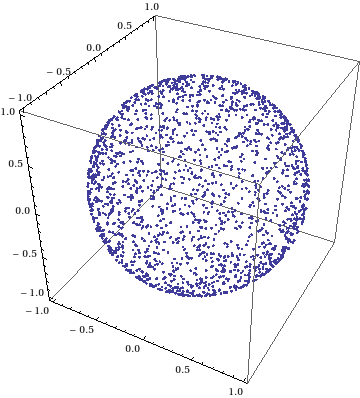
球面上の一様分布
球面上に一様分布するランダムな点を生成したい時、 単純に極座標表示で$\theta$と$\varphi$を一様分布させると、極付近に点が集まってしまう。
data1 = Transpose[{Sin[t] Cos[f], Sin[t] Sin[f], Cos[t]} /. {
f -> RandomReal[{0, 2 Pi}, 2000],
t -> RandomReal[{0, Pi}, 2000]}];
g1 = ListPointPlot3D[data1, BoxRatios -> {1, 1, 1}]
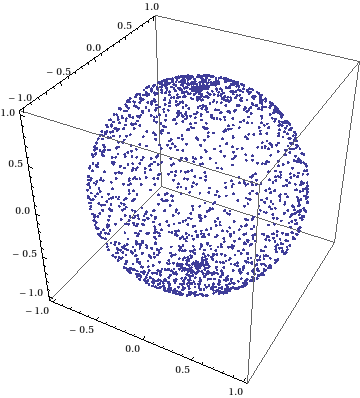
球面上で一様分布させるには、下記のように$\theta$にArcCosを使う
($\theta$の位置の確率を$\sin\theta$に比例させたい→累積確率分布関数は$\cos$→逆関数は$\arccos$)。
data2 = Transpose[{Sin[t] Cos[f], Sin[t] Sin[f], Cos[t]} /. {
f -> RandomReal[{0, 2 Pi}, 2000],
t -> ArcCos[RandomReal[{-1, 1}, 2000]]}];
g2 = ListPointPlot3D[data2, BoxRatios -> {1, 1, 1}]
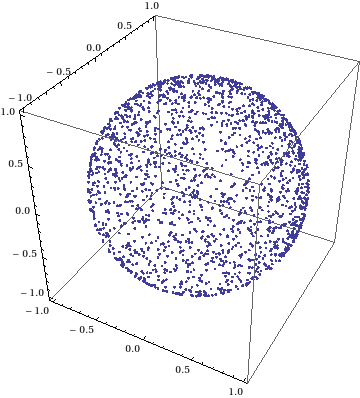
なお、多次元球面上の一様分布は球面上に一様分布する乱数の生成にあるように、 多次元ガウス分布を正規化すると得られる。
下記は3次元の場合。
data3 = Normalize /@ RandomReal[NormalDistribution[], {2000, 3}];
g3 = ListPointPlot3D[data3, BoxRatios -> {1, 1, 1}]