多角形の内外判定
ある点が多角形の内側にあるのか外側にあるのかを判定するには主に
- ある点から直線をひいて多角形の辺と何回交差するか判定する(偶数回なら外、奇数回なら中)
- ある点から多角形の各頂点を順番に見ていったときに何回転するか
の2つの方法がある。
しかし辺との交差回数をカウントするのは、直線と辺が平行だったり、頂点で交差したりする場合などに特別な配慮が必要なので、 ここでは2番目の方法で実装する。
点から多角形上の点を順々に見たときの偏角(反時計まわりを正とする)の和を取ればよいので、ある点Pからみた多角形上の頂点Aから頂点Bまでの偏角∠APBを求める関数をまず作成する。
この実装方法にもベクトルの外積を考えるなど何通りか考えられるが、せっかくMathematicaを使うので楽をして、複素数にしてArgで偏角をとることにする。
Angle[{{x1_, y1_}, {x2_, y2_}, {x3_, y3_}}] :=
Module[{v1 = Complex[x1 - x3, y1 - y3], v2 = Complex[x2 - x3, y2 - y3]},
If[TrueQ[v1 == 0], 0, Arg[v2/v1]]
]
多角形の内外判定はMathematicaのPolygonなどの表示に合わせ、自己交差している場合は内部と外部を交互に繰り返すものとすると、
- 偏角の和が$0, \pm 4\pi, \pm 8\pi, \ldots$のとき点は多角形の外
- 偏角の和が$\pm 2\pi, \pm 6\pi, \pm 10\pi, \ldots$のとき点は多角形の中
とできる。
以上より多角形の内外を判定する関数InsidePolygonQは以下のように実装できる。
InsidePolygonQ[poly : {{_, _} ..}, p : {_, _}] := Module[
{argsum},
argsum = Round[Total[MapThread[Angle[{##, p}] &, {poly, RotateLeft[poly]}]]/(2 Pi)];
OddQ[argsum]
]
丸め誤差が蓄積すると誤判定してしまうのだが、誤判定するために要求される丸め誤差はπなので、多分大丈夫だと思われる。
高速化するためには、以下の書き方がMathematicaらしく簡潔で、なおかつ動作も速い。
InsidePolygonQ2[poly : {{_, _} ..}, p : {_, _}] :=
Block[{a = Complex @@@ poly, b = Complex @@ p},OddQ@Round[Total@Arg[(RotateLeft[a] - b)/(a - b)]/(2 Pi)]]
Oct. 2 2013 追記:
有難いことにこのページがYahoo知恵袋などで結構リンクされているものの、 Mathematicaであるためか分かりにくそうなので、上記関数の使用例を追加。
InsidePolygonQ2[{{0, 0}, {2, 0}, {3, 1}, {1, 2}, {2, 1}}, {1, 0.3}]
True
InsidePolygonQ2[{{0, 0}, {2, 0}, {3, 1}, {1, 2}, {2, 1}}, {1, 0.8}]
False
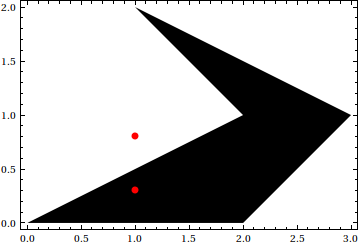
多角形と点の位置関係は下図。(1,0.3)は多角形内部、(1,0.8)は多角形外部である。