(旧)日本測地系から世界測地系への変換式を作ってみる
旧日本測地系(Tokyo Datum)から世界測地系(JGD2000)への変換に関して、既存の1次近似式の確認と、最新のパラメータファイルを使っての新たな近似式の作成を行ってみた。
既存1次式の確認
検索すると出てくるのが以下の1次近似式(latW、lonWが世界測地系の緯度経度、lat、lonは旧日本測地系の緯度経度)。
latW = lat - 0.00010695 * lat + 0.000017464 * lon + 0.0046017lonW = lon - 0.000046038 * lat - 0.000083043 * lon + 0.0100400
出典を明記していないままこの式を記載しているページが非常に多いのだが、念入りに探してみると、Internet ArchiveのWeyback Machineに保存されていたページを見つけた→02 DATUM。
このページはNowral氏という方が作ったもので、Wayback Machineの記録によると遅くとも2004年5月28日の時点ではこの式が既に存在していた(ページの他の個所の記述を見ると1999年ごろに作られた?)。 2005年11月17日のGoogleグループの投稿(APIにおける世界測地系)が初出としているページも見受けられたが、Nowral氏のほうが古い。 残念ながら2014年7月10日から2015年11月16日の間に削除されてしまったようだ。
さて、この式が何をもとに作られたのか、というと、当時の国土地理院が発表していた地域ごとの変換パラメータ(座標系変換パラメータ)に対してフィッティングを行ったものとのこと。
このパラメータが提供されるのは本土四島の領域のみで沖縄県や鹿児島県の離島部については与えられておらず、またメッシュは緯度方向に40分単位、経度方向に1度単位で与えられていた。
座標系変換パラメータをテキスト化したTKY2WGS.TXTを利用させていただいてMathematicaで1次式にフィッティングすると、
tky2wgsdata = Import["TKY2WGS.TXT","Table"][[2;;]];
dBwgs = {IntegerPart[#[[1]]]+FractionalPart[#[[1]]]*(5/3)+1/3,IntegerPart[#[[2]]]+FractionalPart[#[[2]]]*(5/3)+0.5,#[[3]]/3600}& /@ tky2wgsdata;
dLwgs = {IntegerPart[#[[1]]]+FractionalPart[#[[1]]]*(5/3)+1/3,IntegerPart[#[[2]]]+FractionalPart[#[[2]]]*(5/3)+0.5,#[[4]]/3600}& /@ tky2wgsdata;
Fit[dBwgs,{1,lat,lon},{lat,lon}] // InputForm
Fit[dLwgs,{1,lat,lon},{lat,lon}] // InputForm
0.004601672567313928 - 0.00010694812329117429*lat + 0.00001746361043217061*lon
0.01003997982991391 - 0.000046038306090388064*lat - 0.00008304294296247845*lon
となり、確かにNowral氏の1次式は座標系変換パラメータから得られた式であった。
また、この式は基準回転楕円体の変更(BesselからGRS80)と地球中心位置の平行移動のほか、三角測量網の歪みと地殻変動による影響を考慮した変換式であることが確認できた。
最新のデータを使ってフィッティングしてみる
現在は南西諸島や小笠原諸島を含み、より細かいメッシュ(緯度方向に30秒、経度方向に45秒)でデータが与えられたTKY2JGD.parが国土地理院から配布されている(TKY2JGD for Windowsダウンロード | 国土地理院)。
これを使えば、もしかしたら近似式の精度を改善できるかもしれない、ということで1次~3次式でフィッティングしてみた。
TKY2JGD.PARのバージョンはWeb版のTKY2JGD Ver.1.3.80が利用する2.1.1を利用した。
ただし、宮古島以西、大東諸島、八丈島、青ヶ島は周辺地域と比べて極端にずれているため除外した(以降の誤差評価でも除いている)。
同様にMathematicaでフィッティングし、以下の近似式が得られた。
- 1次式
latW = lat + 0.00442664394367075 - 0.00010830028219110943*lat + 0.000019074856883090637*lonlonW = lon + 0.010402901691807681 - 0.000043254037811818526*lat - 0.00008647891424484744*lon
- 2次式
latW = lat + 0.016477522152087188 - 0.000017789134840406895*lat - 3.7999795449370385e-7*lat^2 - 0.00018138325650007267*lon - 4.46725604751588e-7*lat*lon + 7.909460428663596e-7*lon^2lonW = lon + 0.006184787179550604 - 0.000011557674383667673*lat - 9.74833404431774e-7*lat^2 - 0.000031734077330480837*lon + 3.258192351492716e-7*lat*lon - 2.534232516398711e-7*lon^2
- 3次式
latW = lat - 0.060900059135008414 + 0.003361617191066646*lat + 1.2795747406005985e-6*lat^2 + 5.201225639893501e-8*lat^3 + 0.0006051338742218461*lon - 0.000050694419571524394*lat*lon - 5.023128450118049e-8*lat^2*lon + 1.8148757567289107e-6*lon^2 + 1.9557426585832626e-7*lat*lon^2 - 1.992482916686384e-8*lon^3lonW = lon - 0.13994168800009116 + 0.0013927217169657682*lat + 0.0000138161256143156*lat^2 - 1.0901155011294384e-7*lat^3 + 0.002792369979389253*lon - 0.000027625021457358877*lat*lon - 1.6982726079231825e-8*lat^2*lon - 0.000017166797196903788*lon^2 + 1.0415388590600207e-7*lat*lon^2 + 3.2095893780347566e-8*lon^3
もともとの1次近似式と、新たに作成した上の3式の誤差を比較すると、下表のようになった。
ここでは誤差を「TKY2JGD.parで与えられる地点において、近似式による変換後の緯度経度と、TKY2JGDによる変換後の緯度経度との測地線距離(m)」として計算した。
| 近似式 | 誤差分布 | 誤差 |
|---|---|---|
| Nowral氏1次式 | 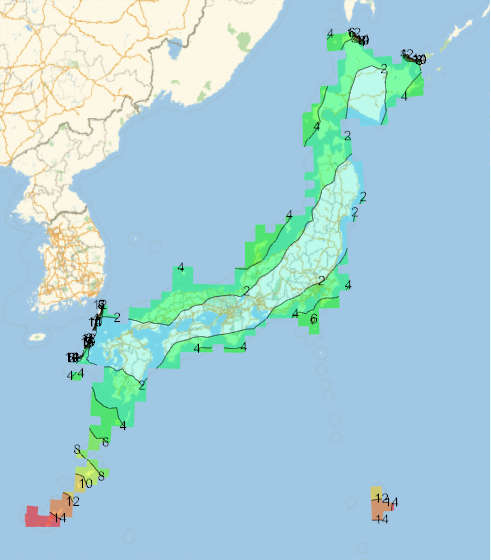
|
最大誤差: 15.68m 平均誤差: 2.01m |
| 1次式 | 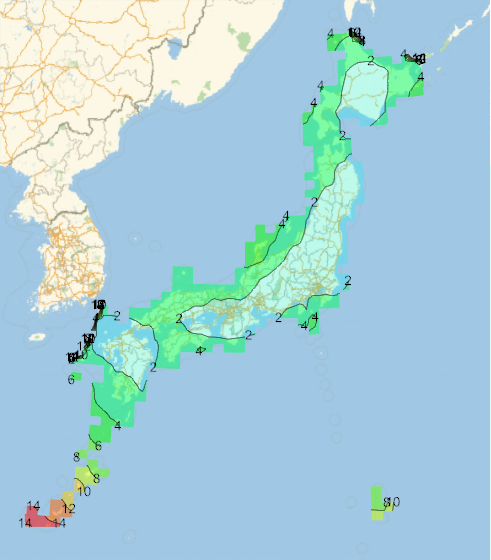
|
最大誤差: 15.15m 平均誤差: 1.79m |
| 2次式 | 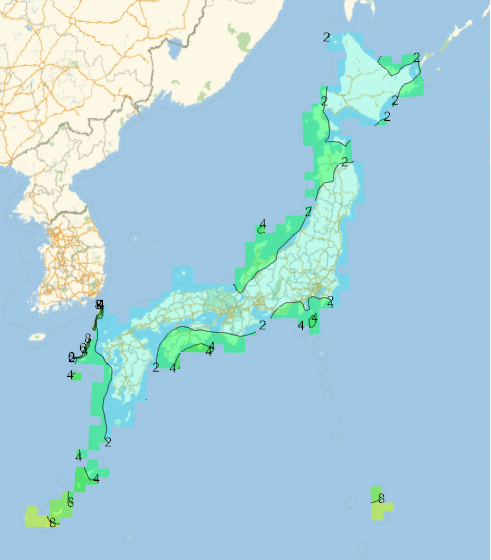
|
最大誤差: 9.88m 平均誤差: 1.41m |
| 3次式 | 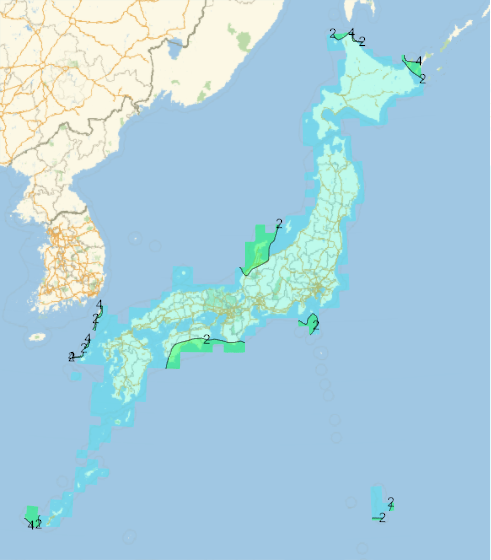
|
最大誤差: 4.04m 平均誤差: 0.69m |
目論見通り、TKY2JGD.PARをフィッティングして得られた1次式はNowral氏の1次式と比較して若干改善できた。
ただ、その改善幅は平均で22cmと大きくはなく、また南西諸島で15m程度の誤差が出てしまう弱点は共通しているため、Nowral氏の1次式を置き換えて利用できるものにはならなかった。
一方で、次数を上げるにつれて誤差を小さくでき、3次式では南西諸島と小笠原諸島での誤差が2m程度まで抑えられたため、使える場面があるかもしれない(宮古島以西と大東諸島、八丈島、青ヶ島では使えない点は注意)。