Mathematica

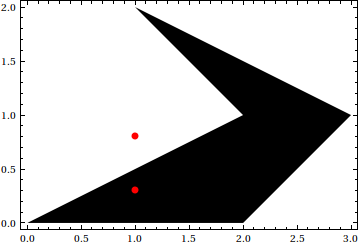
ある点が多角形の内側にあるのか外側にあるのかを判定するには主に ある点から直線をひいて多角形の辺と何回交差するか判定する(偶数回なら外、奇数回なら中) ある点から多角形の各頂点を順番に見ていったときに何回転するか の2つの方法がある。 しかし辺との交差回数をカウントするのは、直線と辺が平行だったり、頂点で交差したりする場合などに特別な配慮が必要なので、 ここでは2番目の方法で実装する。 点から多角形上の点を順

FORTRANで書かれた古いMS-DOSプログラムを.NET/Linkを使ってMathematicaから操るパッケージを作っていたところ、 Process.StartInfo.RedirectStandardInputやRedirectStandardOutputにTrueを設定してもまったく標準入出力をリダイレクトできなかった。(※OSはVista 32bit) いろいろ試してみたところ、16ビットのプログラム

MathematicaでGPXファイルを読み込んで解釈する方法のメモ。 対象となるGPXファイルを xml = Import[filepath, "XML"]; でまずXMLとして読み込んでおいて、 trk = Cases[xml, XMLElement["trk", _, _], Infinity]; でtrk要素を抜き出し、 trkpt = (ToExpression[{"lat", "lon"} /. Cases[#1, XMLElement["trkpt", attr_, _] :> attr, Infinity]] & ) /@ trk; でそれぞれのtrk要素からtrkpt要素を抜き出して緯度と経度を得る。 Sep. 28 2013追記 Mathematica 8からは標準でGPXをImport可能になった。

Mathematicaで友愛数を列挙するプログラム例として以下のようなものが見受けられる。 yakuwa[n_] := DivisorSigma[1, n] - n; Do[If[(yakuwa[yakuwa[k]] == k) && (yakuwa[k] != k), Print[{k, yakuwa[k]}]], {k, 1, 1000}]; しかし、Doでループを回してPrintで書き出していくのはMathematica的に美しくないと思う。 Mathematicaなら関数型プログラミングとパターンマッチを用いるのが良いと思うので、私なら以下のように書く。 Cases[NestList[DivisorSigma[1, #] - # &, #, 2] & /@ Range[100000], {a_, b_, a_} /; a < b -> {a, b}] 実行速度もこちらの

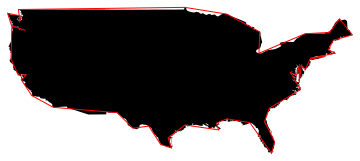
読み込んだGPSログのデータを間引きたい、と思って調べたところ、 (Ramer-)Douglas-Peuckerのアルゴリズムというものがあることが分かった。

基本的な考え方は、

1. 折れ線の始点と終点を結ぶ線分と各点の距離を求める。
2. すべての点との距離が許容誤差$\varepsilon$以内に入っていれば始点と終点だけを返して終了。
3. そうでなければ距離が最大の点Pを選択。
4. 始点から点Pまでの折れ線と、点Pから終点までの折れ線のそれぞれについてまた1から処理する。

という再帰的なもの。

再帰的なものはMathematicaの得意分野なので、MathematicaでRamer-Douglas-Peuckerのアルゴリズムを実装してみた。